本文介绍 Microsoft Excel 中 CONFIDENCE.NORM 函数的公式语法和用法。

说明

置信区间为某一范围的值。 样本平均值 x 位于此范围的中心，此范围为 x ± CONFIDENCE.NORM。 例如，如果 x 是通过邮件订购的产品交付时间的样本平均值，x ± CONFIDENCE.NORM 为总体平均值范围。 对于在此范围中的任意总体平均值 μ0，从 μ0 而非 x 中获取样本平均值的概率大于 alpha；对于不在此范围内的任意总体平均值 μ0，从 μ0 而非 x 中获取样本平均值的概率小于 alpha。 换言之，假设我们使用 x、standard_dev 和字号在显著性水平 alpha 上构建一个双尾测试，其中假设总体平均值为 μ0。 则如果 μ0 处于置信区间，我们将不会拒绝该假设；如果 μ0 未处于置信区间，则将拒绝该假设。 置信区间无法使我们推断出概率 1 - alpha，即我们的下一个包的发送时间处于置信区间内。

语法

CONFIDENCE.NORM(alpha,standard_dev,size)

CONFIDENCE.NORM 函数语法具有下列参数：

• Alpha 必需。 用来计算置信水平的显著性水平。 置信水平等于 100*(1 - alpha)%，亦即，如果 alpha 为 0.05，则置信水平为 95%。

• standard_dev 必需。 数据区域的总体标准偏差，假定为已知。

• 大小 必需。 样本大小。

备注

• 如果任意参数为非数值型，则 CONFIDENCE.NORM 返回 #VALUE! 错误值 #REF!。

• 如果 alpha ≤ 0 或 alpha ≥ 1，则 CONFIDENCE.NORM 返回 #NUM! 错误值 #REF!。

• 如果 standard_dev ≤ 0，则 CONFIDENCE.NORM 返回 #NUM! 错误值 #REF!。

• 如果 size 不是整数，将被截尾取整。

• 如果 size < 1，则 CONFIDENCE.NORM 返回 #NUM! 错误值 #REF!。

• 如果假设 alpha 等于 0.05，则需要计算等于 (1 - alpha) 或 95% 的标准正态分布曲线之下的面积。 其面积值为 ±1.96。 因此置信区间为：

  

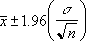
复制下表中的示例数据，然后将其粘贴进新的 Excel 工作表的 A1 单元格中。要使公式显示结果，请选中它们，按 F2，然后按 Enter。如果需要，可调整列宽以查看所有数据。

数据	说明
0.05	显著水平参数
2.5	总体标准偏差
50	样本容量
公式	说明	结果
=CONFIDENCE.NORM(A2,A3,A4)	总体平均值的置信区间。 换言之，花在上班路上的基础总体平均时间的置信区间为 30 ± 0.692952 分钟，或 29.3 到 30.7 分钟。	0.692952