本文介绍 Microsoft Excel 中 NEGBINOM.DIST 函数的公式语法和用法。

说明

返回负二项式分布，即当成功概率为 Probability_s 时，在 Number_s 次成功之前出现 Number_f 次失败的概率。

此函数与二项式分布相似，只是它的成功次数固定，试验次数为变量。 与二项式分布相同的是，二者均假定试验是独立的。

例如，如果要找 10 个反应敏捷的人，且已知候选人符合相关条件的概率为 0.3。 NEGBINOM.DIST 将计算出在找到 10 个合格候选人之前，需面试特定数目的不合格候选人的概率。

语法

NEGBINOM.DIST(number_f,number_s,probability_s,cumulative)

NEGBINOM.DIST 函数语法具有下列参数：

• Number_f 必需。 失败的次数。

• Number_s 必需。 成功次数的阈值。

• Probability_s 必需。 成功的概率。

• cumulative 必需。 决定函数形式的逻辑值。 如果 cumulative 为 TRUE，则 NEGBINOM.DIST 返回累积分布函数；如果为 FALSE，则返回概率密度函数。

备注

• Number_f 和 number_s 将被截尾取整。

• 如果任一参数为非数值型，则 NEGBINOM.DIST 返回 错误值 #VALUE!。

• 如果 probability_s < 0 或 probability > 1，则 NEGBINOM.DIST 返回 错误值 #NUM!。

• 如果 number_f < 0 或 number_s < 1，则 NEGBINOM.DIST 返回 错误值 #NUM!。

• 负二项式分布的公式为：

  

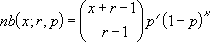
  其中：

  x 是 number_f，r 是 number_s，且 p 是 probability_s。

复制下表中的示例数据，然后将其粘贴进新的 Excel 工作表的 A1 单元格中。要使公式显示结果，请选中它们，按 F2，然后按 Enter。如果需要，可调整列宽以查看所有数据。

数据	说明
10	失败次数
5	成功的极限次数
0.25	成功的概率
公式	说明	结果
=NEGBINOM.DIST(A2,A3,A4,TRUE)	在上述条件下的累积负二项式分布值	0.3135141
=NEGBINOM.DIST(A2,A3,A4,FALSE)	在上述条件下的概率负二项式分布值	0.0550487