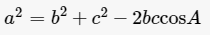
对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
余弦定理是解三角形中的一个重要定理,可应用于以下三种需求: 1、当已知三角形的两边及其夹角,可由余弦定理得出已知角的对边。 2、当已知三角形的三边,可以由余弦定理得到三角形的三个内角。 3、当已知三角形的三边,可以由余弦定理得到三角形的面积。...
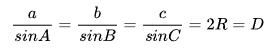
一个三角形中,各边和所对角的正弦之比相等,且该比值等于该三角形外接圆的直径(半径的2倍)长度。正弦定理公式为a/sinA = b/sinB =c/sinC = 2r=D(r为外接圆半径,D为直径)。
历史上,正弦定理的几何推导方法丰富多彩。根据其思路特征,主要可以分为两种。 第一种方法可以称为 “同径法 ”,最早为13世纪阿拉伯数学家、天文学家纳绥尔丁和15世纪德国数学家雷格蒙塔努斯所采用。“同径法 ”是将三角形两个内角的正弦看作半径相同的圆中的正...

① 相交:直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线。 ② 相切:直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点。 ③ 相离:直线和圆没有公共点,这时我们说这条直线和圆相离。...

已知正棱柱的底面周长C,高为L,可以计算出侧面积S的公式。
底面是正多边形的直棱柱叫做正棱柱。 正棱柱是侧棱都垂直于底面,且底面是正多边形的棱柱。 正棱柱一定是直棱柱,而直棱柱不一定是正棱锥。 特别注意:底面为正多边形,侧棱垂直于底面,但是侧棱和底面边长不一定相等。而直棱柱侧棱也是垂直于底面,侧棱和底面边长不一定相等,而且底面多边形形状也不确定。...

已知正棱台上底面积、下底面积、高,可以计算出正棱台体积。
棱台的体积等于这三个棱锥的体积之和: 1.以棱台的高作高,它的下底作底的; 2.以棱台的高作高,它的上底作底的; 3.以棱台的高作高,它的上下两底面积的比例中项作底的。...

已知正棱台上底周长C1,下底周长C2,斜高h,计算侧面积S的公式。
正棱台图示 正棱台的侧面展开图 正棱台的侧面展开是由各个侧面组成的平面图形,它是由一些有公共顶点的等腰梯形组成的,这个公共顶点即为等腰梯形两腰延长后的交点。等腰梯形的上、下底就是正棱台上、下底面边长.等腰梯形的腰就是正棱台的侧棱长。 用一个平行于棱锥底面的平面去截棱锥,介于底面和截面之间的部分叫做...

圆台:以直角梯形垂直于底边的腰所在直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫做圆台.旋转轴叫做圆台的轴.直角梯形上、下底旋转所成的圆面称为圆台的上、下底面,另一腰旋转所成的曲面称为圆台的侧面,侧面上各个位置的直角梯形的腰称为圆台的母线,圆台的轴上的梯形的腰的长度叫做圆台的高,圆台的高也...


